Resolución de inecuaciones lineales, de segundo grado y racionales

Introducción

Una inecuación es una relación de desigualdad entre dos expresiones algebraicas en las que aparece una o más incógnitas. Resolver una inecuación consiste en encontrar todos los valores de la incógnita para los que se cumple la relación de desigualdad.
Los signos de desigualdad que se utilizan en las inecuaciones son: $<$, $>$, $\le$ y $\ge$:

• a < b significa "a es menor estrictamente que b". Por ejemplo: 2 < 3.
• a > b significa "a es mayor estrictamente que b". Por ejemplo: 3 > 2.
• a ≤ b significa "a es menor o igual que b". Por ejemplo: 2 ≤ 2.
• a ≥ b significa "a es mayor o igual que b". Por ejemplo: 3 ≥ 2.

Nota: se dice que los signos $<$ y $>$ son estrictos porque no puede darse la igualdad. Es decir, indican "menor" y "mayor", respectivamente, pero nunca "igual".

2. Solución de una inecuación

La solución de una inecuación es el valor o conjunto de valores que puede tomar la incógnita $x$ para que se cumpla la inecuación. A diferencia de las ecuación (cuyo signo es "="), no podemos saber de antemano el número de soluciones.
Puede darse el caso en que la solución es sólo un punto (por ejemplo, $x=2$), un intervalo (por ejemplo, $x\in [0,2]$), una unión de intervalos o que no exista ninguna solución.

3. Tipos de inecuaciones

Inecuación lineal: cuando las expresiones de ambos lados son polinomios de primer grado.

Ejemplo:

$$x+2\le 0$$

La solución de esta inecuación es el intervalo $(-\infty ,-2]$.

Inecuación de segundo grado: cuando las expresiones de ambos lados son polinomios de grado menor o igual que 2.

Ejemplo:

$$x^2<0$$

Esta inecuación no tiene soluciones (reales) puesto que ningún número al cuadrado es negativo.

Inecuación racional: cuando las expresiones de uno o ambos lados son un cociente de polinomios.

Ejemplo:

$$\frac{2}{x}\le 0$$

La solución de esta inecuación es $x\in (-\infty ,0)$.

Inecuación con valor absoluto: cuando en las expresiones algebraicas hay valores absolutos.

Ejemplo:

$$|x|<0$$

Esta inecuación no tiene solución porque el módulo (valor absoluto) de un número es siempre mayor o igual que 0.
Resolvemos este tipo de inecuaciones en otra página:

Valor absoluto e inecuaciones

4. Nota previa (para resolver inecuaciones)

La metodología de resolución es análoga a la de las ecuaciones, pero teniendo siempre en cuenta que se trata de una desigualdad. Esto supone, por ejemplo, cambiar el signo de desigualdad cada vez que multiplicamos o dividimos por un negativo para mantener la relación.

Ejemplo:

$$2\le 3$$

Para multiplicar por un negativo, por ejemplo, -2, cambiamos la desigualdad al resultado:

$$-2\cdot 2\ge -2\cdot 3$$

$$-4\ge -6$$

Notemos que si no la cambiamos, obtenemos una relación falsa ($-4\le -6$).

Intervalos: en los intervalos utilizaremos los símbolos "$($" y "$[$" para el extremo izquierdo y los símbolos "$)$" y "$]$" para el extremo derecho. Los paréntesis indican que el extremo está incluido en el intervalo y los corchetes indican lo contrario.
Por ejemplo, el intervalo $(2,3)$ están incluido en el intervalo $[2,3)$, pero también en $(2,3]$ y en $[2,3]$. Sin embargo, el intervalo $[2,3)$ no está incluido en $(2,3]$ ni en $(2,3)$.
Para expresar la unión de dos o más intervalos utilizamos el símbolo $\cup$.

5. Inecuaciones lineales resueltas

Inecuación 1

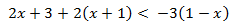
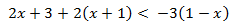
Solución

Inecuación 2

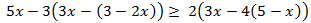
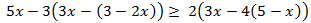
Solución

Inecuación 3

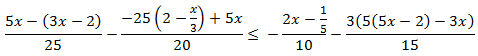
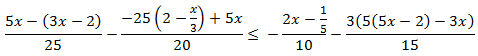
Solución

Inecuación 4

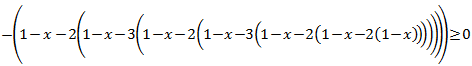
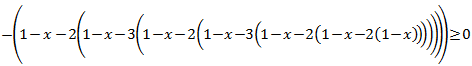
Solución

Inecuación 5

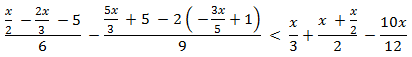
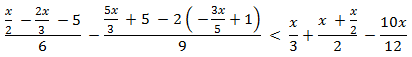
Solución

6. Inecuaciones de segundo grado resueltas

Inecuación 1

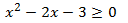
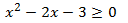
Solución

Inecuación 2

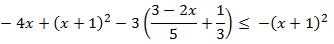
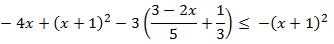
Solución

Inecuación 3

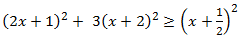
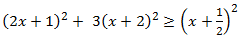
Solución

Inecuación 4

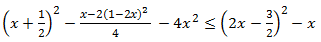
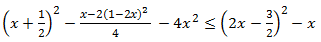
Solución

Inecuación 5

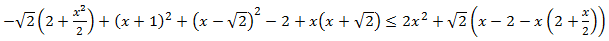
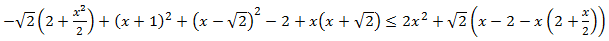
Solución

7. Inecuaciones racionales resueltas

Inecuación 1

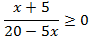
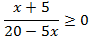
Solución

Inecuación 2

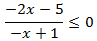
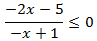
Solución

Inecuación 3

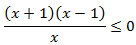
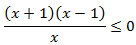
Solución

Inecuación 4

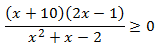
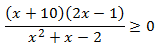
Solución

Inecuación 5

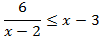
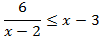
Solución

https://www.matesfacil.com/ESO/inecuaciones/ejercicios-resueltos-inecuaciones.html